Tâm đối xứng là gì? Hình nào không có tâm đối xứng? – VOH
Trong bài viết này viethanbinhduong.edu.vn sẽ chia sẻ chuyên sâu kiến thức của Tâm đối xứng là gì để chia sẻ cho bạn đọc
Tâm đối xứng là một khái niệm mới trong chương trình toán THCS. Trong thực tế, có rất nhiều thứ có tâm đối xứng như đĩa tròn, cỏ bốn lá, một viên gạch, thậm chí là một bông hoa. Vậy tâm đối xứng của một hình là gì? Những hình như thế nào là hình có tâm đối xứng? Bài viết dưới đây sẽ giúp các bạn học sinh biết và hiểu rõ về phần kiến thức mới này.
1. Tâm đối xứng là gì?
Những hình có một điểm cố định ở giữa sao cho khi quay nửa vòng quanh điểm đó, ta được vị trí mới của hình sẽ chồng khít với vị trí ban đầu (trước khi quay) thì được gọi là hình có tâm đối xứng và điểm đó cũng chính là là tâm đối xứng của hình.
Quan sát các hình vẽ dưới đây:

Ta nhận thấy, mỗi hình vẽ này đều sẽ có một tâm đối xứng ở giữa
+ Bông hoa có một tâm đối xứng ở chính giữa của bông hoa, nghĩa là ở điểm chính giữa đó, khi ta quay nửa vòng tròn quanh điểm đó thì vị trí mới của bông hoa sẽ chồng khít với vị trí trước khi quay của bông hoa đó.
+ Hoặc với chiếc chong chóng 4 cạnh, ta lấy điểm cố định ở giữa, sau khi từ điểm cố định đó quay một nửa vòng tròn thì ta sẽ được vị trí mới của chong chóng chồng khít với vị trí ban đầu khi chưa quay của chong chóng.
Như vậy, cả bông hoa và chong chóng 4 cạnh ở đây đều là hình có tâm đối xứng
1.1. Tâm đối xứng của đoạn thẳng
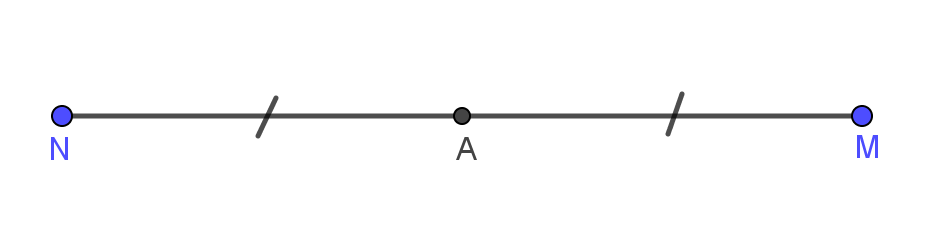
Cho đoạn thẳng MN với A là trung điểm của MN. Khi đó A chính là tâm đối xứng của đoạn thẳng MN. Nghĩa là từ điểm A ta quay nửa vòng tròn, ta sẽ được một đoạn thẳng chồng khít với đoạn thẳng MN ban đầu.
Hình vẽ minh họa
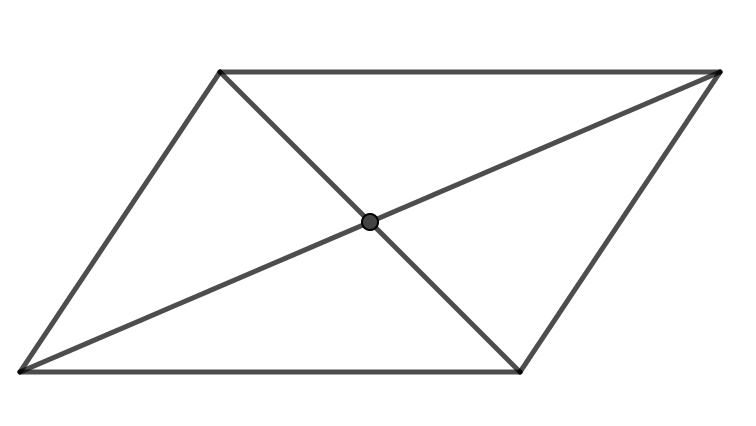
1.2. Tâm đối xứng của hình bình hành, hình vuông, hình chữ nhật, hình thoi
Tâm đối xứng của hình bình hành, hình vuông, hình chữ nhật, hình thoi chính là giao điểm hai đường chéo của các hình đó.
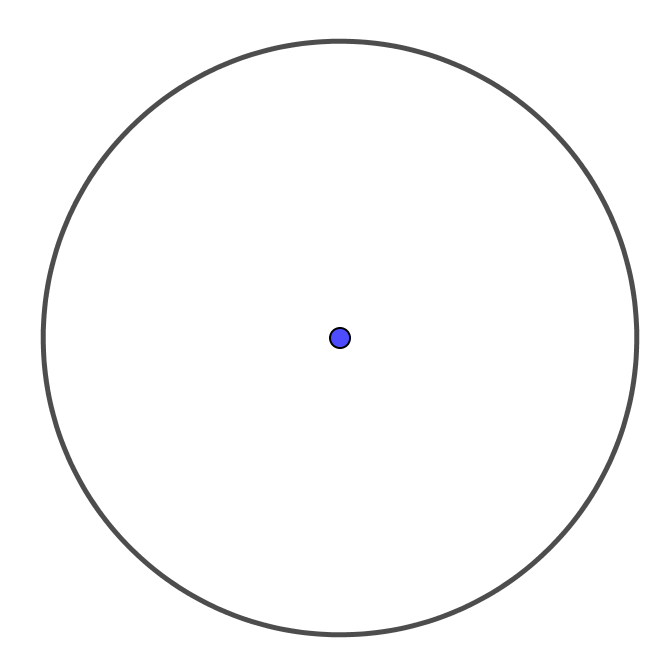
1.3. Tâm đối xứng của hình tròn
Tâm đối xứng của hình tròn là tâm của hình tròn đó.
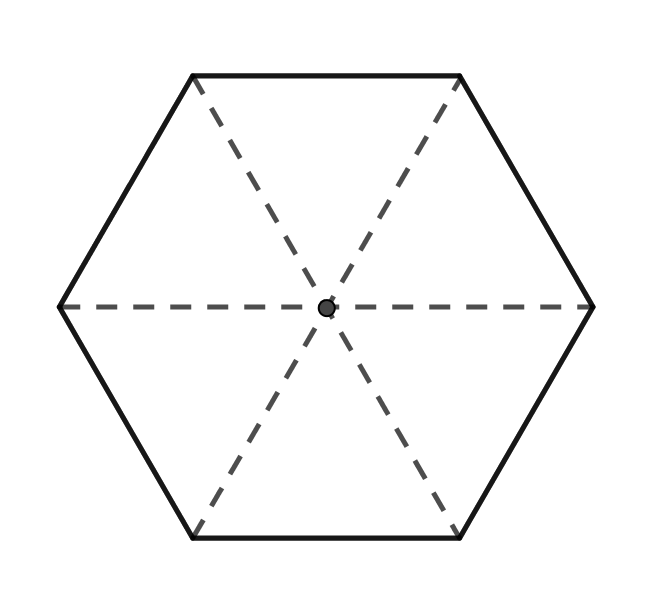
1.4. Tâm đối xứng của hình lục giác đều
Tâm đối xứng của hình lục giác đều chính là giao điểm của các đường chéo chính.
*Lưu ý: Tam giác đều, tam giác cân, ngũ giác đều, hình thang cân đều không có tâm đối xứng
1.5. Tâm đối xứng của một số chữ cái in hoa
Có những chữ cái in hoa cũng có tâm đối xứng
Tham khảo các hình vẽ dưới đây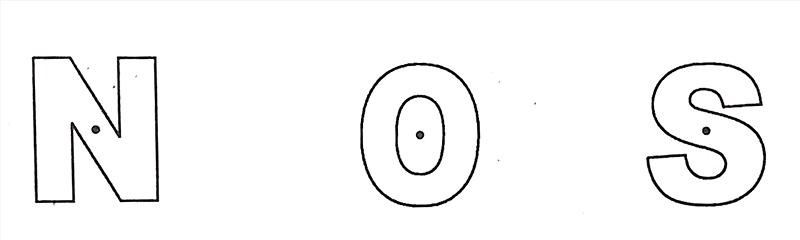
*Chú ý: Mỗi hình chỉ có nhiều nhất là 1 tâm đối xứng
2. Bài tập về tâm đối xứng lớp 6
Bài 1. Điền từ thích hơp còn thiếu vào chỗ trống dưới đây
- Tâm đối xứng của đoạn thằng là … của đoạn thẳng đó
- Tâm đối xứng của hình bình hành, hình chữ nhật, hình thoi, hình vuông là …. của đường chéo
- Tâm đối xứng của hình tròn là … của đường tròn đó
- Tâm đối xứng của lục giác đều là … của đường chéo chính của lục giác đều đó
- Tam giác vuông, tam giác cân … tâm đối xứng
- Hình thang cân … tâm đối xứng
- Mỗi hình có nhiều nhất là … tâm đối xứng
ĐÁP ÁN
a, Tâm đối xứng của đoạn thẳng là trung điểm của đoạn thẳng đó
b, Tâm đối xứng của hình bình hành, hình chữ nhật, hình thoi, hình vuông là giao điểm của đường chéo
c, Tâm đối xứng của hình tròn là tâm của đường tròn đó
d, Tâm đối xứng của lục giác đều là giao điểm của các đường chéo chính của lục giác đều đó
e, Tam giác vuông, tam giác đều, tam giác cân đều không có tâm đối xứng
f, Hình thang cân không có tâm đối xứng
g, Mỗi hình có nhiều nhất là một tâm đối xứng
Bài 2. Trong các hình dưới đây, hình nào có tâm đối xứng, hình nào không có tâm đối xứng. Nếu có hãy chỉ ra tâm đối xứng của hình đó.







ĐÁP ÁN
– Hình 1: là dạng hình tròn, có tâm đối xứng là điểm chính giữa của hình đó. Khi từ điểm chính giữa đó quay nửa vòng tròn ta sẽ được vị trí mới của hình chồng khít với vị trí ban đầu khi chưa quay của nó.
– Hình 2: Ngôi sao 5 cánh là hình không có tâm đối xứng. Không có điểm nào để khi quay nửa vòng tròn thì ngôi sao đó sẽ có vị trí chồng khít với vị trí ban đầu khi chưa quay của ngôi sao 5 cánh
– Hình 3: cỏ 4 lá là một hình có tâm đối xứng, tâm đối xứng chính là điểm chính giữa của bông hoa, từ điểm đó khi ta quay một nửa vòng tròn thì vị trí mới của bông hoa sẽ chồng khít với vị trí ban đầu khi chưa quay của bông hoa đó
– Hình 4: Chữ K là chữ cái không có tâm đối xứng. Không có điểm nào để khi quay nửa vòng tròn thì chữ K đó sẽ có vị trí chồng khít với vị trí ban đầu của chữ K khi chưa quay của chữ K.
– Hình 5: Những chiếc lá đó là hình không có tâm đối xứng. Vì không có điểm nào để khi quay nửa vòng tròn thì chiếc lá đó sẽ có vị trí chồng khít với vị trí ban đầu khi chưa quay của chiếc lá
– Hình 6: Lát cam là một hình có tâm đối xứng, tâm đối xứng chính là điểm chính giữa của lát cam đó, từ điểm đó khi ta quay một nửa vòng tròn thì vị trí mới của lát cam sẽ chồng khít với vị trí ban đầu khi chưa quay của lát cam đó.
– Hình 7: Hình cánh quạt là một hình có tâm đối xứng, tâm đối xứng chính là điểm chính giữa của cánh quạt đó, từ điểm đó khi ta quay một nửa vòng tròn thì vị trí mới của cánh quạt sẽ chồng khít với vị trí ban đầu khi chưa quay của cánh quạt đó.
– Hình 8: Hình trái tim là hình không có tâm đối xứng. Vì không có điểm nào để khi quay nửa vòng tròn thì hình trái tim đó sẽ có vị trí chồng khít với vị trí ban đầu khi chưa quay của hình trái tim
Như vậy, bài viết này đã tổng hợp đầy đủ lý thuyết về tâm đối xứng, hình có tâm đối xứng và hình có tâm đối xứng trong thực tế. Hy vọng sẽ giúp các bạn học sinh trong quá trình học phần kiến thức này.
Chịu trách nhiệm nội dung: GV Nguyễn Thị Trang

