Cách tính thể tích hình nón, diện tích xung quanh và toàn phần hình nó
Trong bài viết này viethanbinhduong.edu.vn sẽ chia sẻ chuyên sâu kiến thức của Công thức tính diện tích hình nón để chia sẻ cho bạn đọc
Trong tổng hợp công thức tính diện tích và thể tích hình nón trong bài viết này, Taimienphi.vn sẽ giới thiệu và chia sẻ chi tiết tới bạn đọc công thức tính diện tích và thể tích hình nón, cách tính và ví dụ cụ thể để tính diện tích và thể tích hình nón.

Hình nón đỉnh A được tạo ra bởi khi quay tam giác OAC vuông tại O,cạnh OA cố định. Các bạn đọc tham khảo thêm trên Wikipedia bài viết về hình nón để hiểu hơn.
1. Công thức và cách tính diện tích hình nón
1.1. Công thức tính diện tích xung quanh hình nón: Diện tích xung quanh hình nón bằng bán kính mặt đáy nhân với độ dài đường sinh và giá trị Pi.
Sxq = π x r x l
Trong đó:
– r : Bán kính mặt đáy của hình nón.– l: Độ dài đường sinh của hình nón.– π: số Pi (xấp xỉ 3,14).
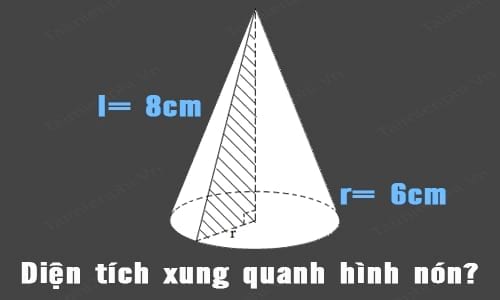
* Ví dụ cách tính diện tích xung quanh hình nón:
Cho một hình nón bất kỳ có đáy là tâm O và đỉnh A. Bán kính r bằng 6cm . Hỏi diện tích xung quanh của hình nón bằng bao nhiêu, biết chiều dài đường sinh nối từ đỉnh A xuống một điểm bất kỳ trên đáy dài 8cm.

Tiếp tục áp dụng theo công thức tính diện tích xung quanh của hình nón, ta có:
Sxq = π x r x l = π x 6 x 8 = 150,72 (cm2).
Đáp án sau khi áp dụng công thức tính diện tích xung quanh hình nón là 150,72 cm2.
1.2. Công thức tính diện tích toàn phần hình nón: Công thức tính diện tích toàn phần của hình nón bằng bán kính mặt đáy nhân với độ dài đường sinh và giá trị Pi.
Stoàn phần = Sxq +Sđáy = π x r x l + π x r2
Trong đó:
– r : Bán kính mặt đáy của hình nón.– l : Độ dài đường sinh của hình nón.– π: số Pi (xấp xỉ 3,14).
* Ví dụ cách tính diện tích toàn phần hình nón
Vẫn tương tự như ví dụ trên, nhưng thay giá trị bán kính r bằng 6cm. Đường sinh dài 8cm. Hỏi diện tích toàn phần của hình nón bằng bao nhiêu?
Áp dụng theo công thức tính diện tích hình nón trên, ta có:
Stoàn phần = π x r x l + π x r2 = π x 5 x 7 + π x 52 = 188,4 (cm2).
Như vậy sau khi áp dụng cách tính diện tích toàn phần của hình nón trên, ta có đáp án là 188,4cm2.
2. Công thức và cách tính thể tích hình nón
* Công thức tính thể tích hình nón
V = 1/3 x π x r2 x h
Trong đó:
– r : Bán kính mặt đáy của hình nón.– h : Chiều cao nối giữa đáy và đỉnh của hình nón.– π: số Pi (xấp xỉ 3,14).
* Ví dụ cách tính thể tích hình nón
Sử dụng tương tự câu hỏi trên, tuy nhiên ta thay đổi một số giá trị của hình nón bao gồm bán kính r bằng 7cm, chiều cao nối từ tâm đáy tới đỉnh của hình nón dài 9cm. Hỏi thể tích hình nón này bằng bao nhiêu.
Sử dụng công thức tính thể tích hình nón trên, ta có thể tích hình nón trên:
V = 1/3 x π x r2 x h = 1/3 x π x (7×7) x 9 ~ 462 cm3.
Trên đây là toàn bộ công thức tính diện tích, thể tích hình nón và việc nắm được các công thức này rất quan trọng khi giải quyết các bài toán liên quan đến hình nón trong trường học và thực tế đời sống.
Đặc biệt trong nhiều bài toán phức tạp, yêu cầu phải kết hợp các công thức tính diện tích hình vuông hay tính thể tích hình lập phương, hình trụ, nếu như bạn nắm được mối tương quan trong công thức tính diện tích hình nón, thể tích hình nón và công thức tính diện tích hình vuông, bạn có thể dễ dàng tìm được các giá trị còn thiếu nếu đề bài chưa cung cấp.
Cùng với hình học không gian, hình trụ, hình hình lập phương được sử dụng khá nhiều, trong đó công thức tính thể tích hình lập phương, hình trụ được yêu cầu sử dụng nhiều nhất và luôn được áp dụng trong các bài toán khó, có điểm số cao. Hy vọng với công thức tính diện tích hình nón, và thể tích hình nón trên trong bài viết, bạn đọc sẽ có cơ sở để giải nhiều hơn các bài toán khó.
https://thuthuat.taimienphi.vn/cach-tinh-the-tich-hinh-non-dien-tich-xung-quanh-va-toan-phan-hinh-non-cong-thuc-tinh-22978n.aspx Hình hộp chữ nhật cũng là một trong những dạng hình học mà bạn phải học qua, cách tính thể tích hình hộp chữ nhật cũng tương đối dễ hiểu và các bạn học sinh, nếu chưa biết công thức tính thể tích hình hộp chữ nhật, mời các bạn theo dõi bài viết trênTaimienphi để biết chính xác công thức của nó nhé.

